Chebyshev Circles: Rotated Roots of Unity and Chebyshev Polynomials

Introduction

The Chebyshev polynomials of the first kind, denoted $T_N(x)$, form one of the most important families of orthogonal polynomials, with applications spanning approximation theory, numerical analysis, and harmonic analysis~[mason2002chebyshev,rivlin1990chebyshev]. These polynomials are typically defined either through the trigonometric identity

\begin{equation}...\end{equation}

or via the three-term recurrence relation

\begin{equation}...\end{equation}

In this paper, we present a novel geometric construction of Chebyshev polynomials using rotated roots of unity. Consider the $N$-th roots of unity on the complex unit circle:

\begin{equation}...\end{equation}

When these roots are rotated by an angle $\theta$ (equivalently, multiplied by $\e^{i\theta}$) and projected onto the real axis, we obtain the $N$ real numbers

\begin{equation}...\end{equation}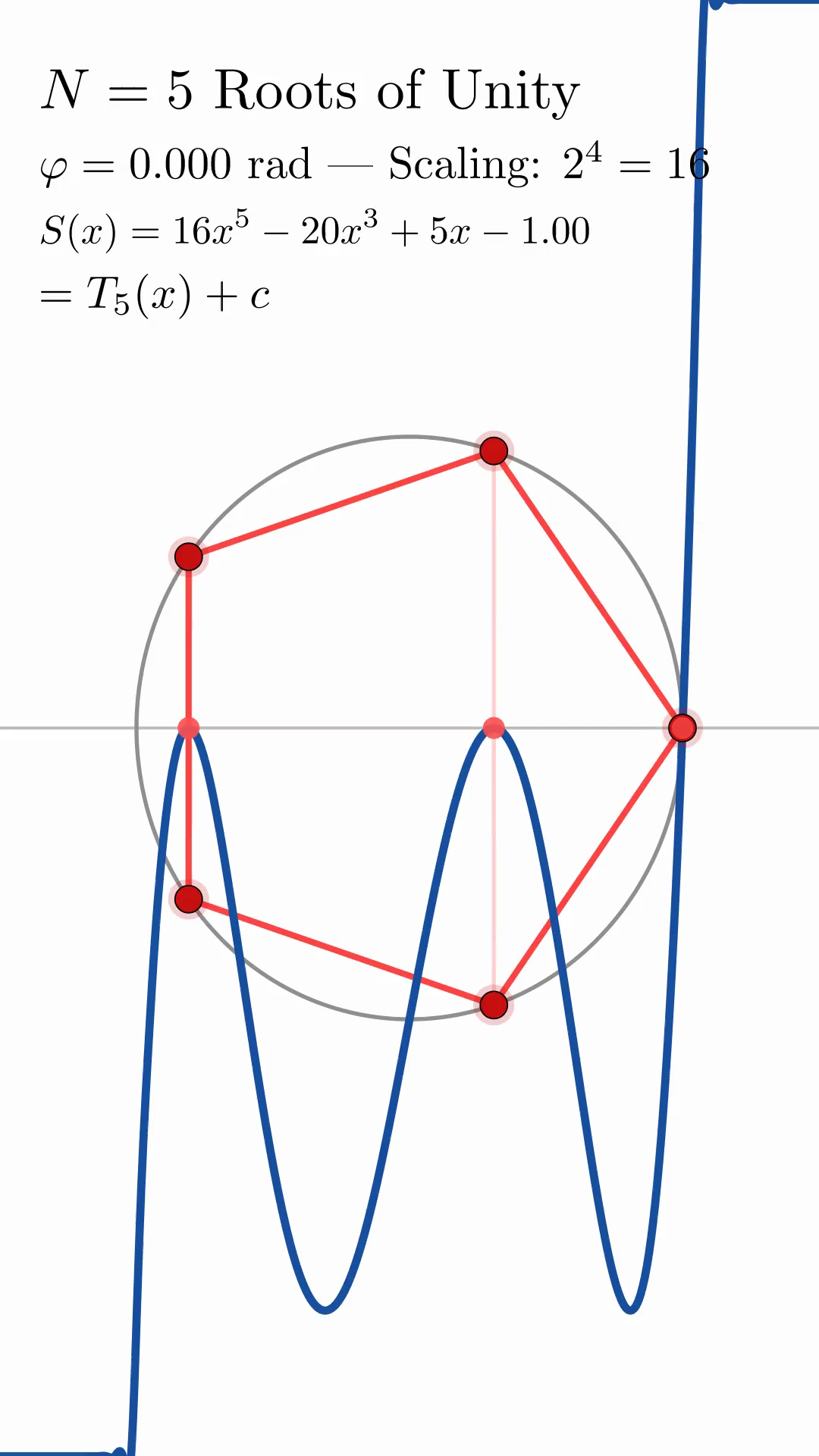

Geometric construction for $N=5$ at rotation angle $\theta = 0$ radians. Red points on the unit circle represent rotated roots of unity; pink points on the real axis are their projections $r_k(\theta)$. The blue curve shows the scaled polynomial $S_N(x; \theta)$ with these projections as roots. Portrait-oriented visualization (1080×1920) generated using Manim Community Edition v0.19.0.

Let $P_N(x; \theta)$ denote the monic polynomial having these projected values as roots:

\begin{equation}...\end{equation}

To match the normalization of Chebyshev polynomials, which have leading coefficient $2^{N-1}$ for $N \geq 1$, we define the scaled polynomial:

\begin{equation}...\end{equation}

Our main result establishes that this construction yields the Chebyshev polynomial up to an additive constant.

Theorem

For any positive integer $N \geq 1$ and any angle $\theta \in \R$,

\begin{equation}...\end{equation}

where the constant $c(\theta)$ is given explicitly by

\begin{equation}...\end{equation}

Moreover, all coefficients of $S_N(x; \theta)$ of degree $k \geq 1$ are independent of $\theta$ and equal the corresponding coefficients of $T_N(x)$.

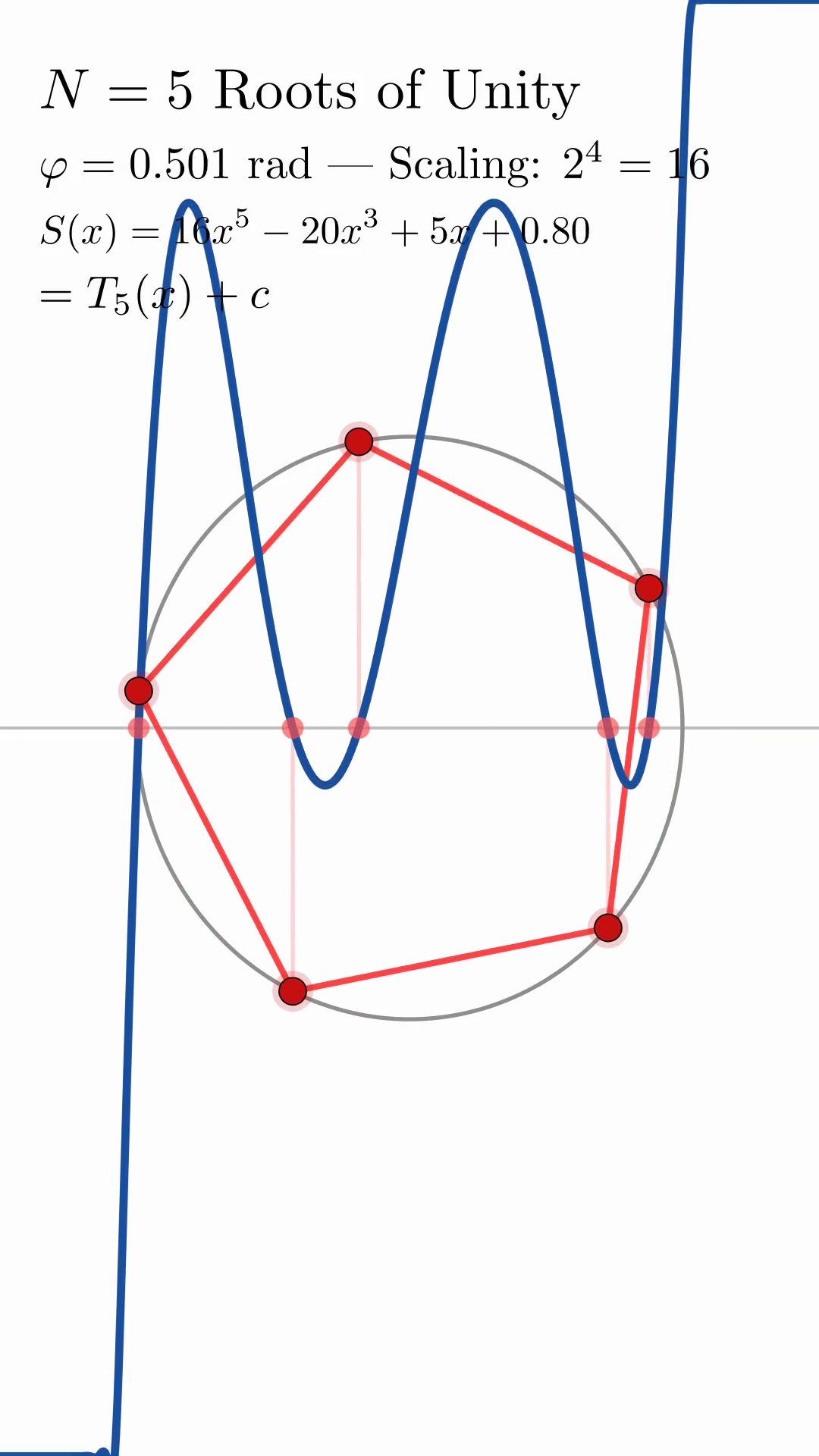
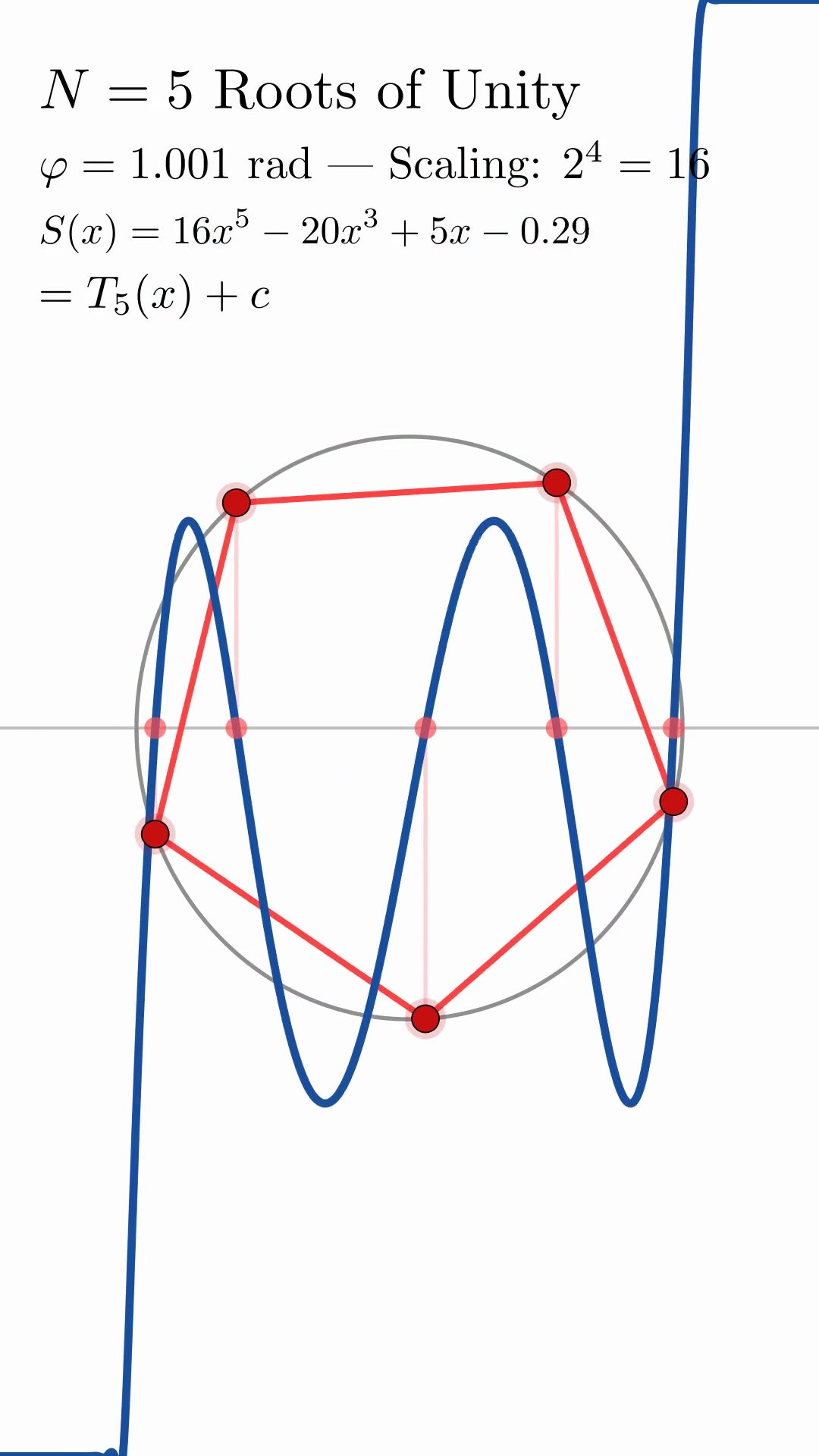
illustrates the geometric construction for $N=5$ at rotation angle $\theta = 0$ radians. As $\theta$ varies, the roots of unity rotate around the unit circle, their projections sweep across the real axis, and the polynomial curve maintains its characteristic Chebyshev shape while only the vertical offset changes. This invariance is demonstrated explicitly in fig:N5_rotation_sequence, which shows the construction at four different rotation angles: $\theta = 0, 0.5, 1.0, \pi/2$ radians. In each panel, the polynomial curve retains the same fifth-degree Chebyshev shape, with only the constant term varying.

Significance and context

This theorem reveals several deep connections:

Discrete geometry meets polynomial theory. The result shows that Chebyshev polynomials emerge naturally from the simplest discrete geometric object---equally-spaced points on a circle---through elementary operations (rotation and projection).
Power sum invariance. The proof hinges on showing that certain discrete sums of powers of cosines are invariant under the phase shift $\theta$. This invariance reflects discrete orthogonality properties of trigonometric functions, a finite analog of continuous Fourier analysis.
Symmetric function theory. Newton's identities provide the bridge from power sums to elementary symmetric polynomials, and hence to polynomial coefficients. The theorem demonstrates this classical algebraic machinery in action.
Roots and quadrature. The projected roots $r_k(0) = \cos(2\pi k/N)$ are closely related to the Chebyshev-Gauss quadrature nodes $\cos((2k+1)\pi/(2N))$, both arising from equidistributed points on the circle.

To our knowledge, this particular geometric construction of Chebyshev polynomials has not appeared explicitly in the literature, though related ideas connecting roots of unity, trigonometric sums, and orthogonal polynomials have long been studied~[szego1939orthogonal,ismail2005classical].

Proof strategy

The proof of thm:main proceeds through several key steps:

Discrete orthogonality (\Cref{sec:orthogonality}). We establish that sums of complex exponentials and cosines over the $N$-th roots of unity satisfy discrete orthogonality relations analogous to Fourier orthogonality.
Power sum invariance (\Cref{sec:power_sums}). Using binomial expansion of $\cos^j(\theta + 2\pi k/N)$ and the orthogonality relations, we prove that the power sums \begin

equation

\sum_

k=0

^

N-1

\cos^j\left(\theta + \frac

2\pi k

N

\right)

are independent of $\theta$ for all $1 \leq j < N$.

We apply Newton's identities to show that if two sets of roots have identical power sums (except for the $0$-th power sum, which counts the number of roots), their elementary symmetric polynomials match. Consequently, the monic polynomials with these roots have identical coefficients except possibly the constant term.

We identify the roots of $T_N(x)$ as $\cos((2k+1)\pi/(2N))$ for $k = 0, \ldots, N-1$, and verify that these roots have the same power sums as the rotated roots $r_k(\theta)$. This establishes coefficient-wise equality for degrees $k \geq 1$.

For $\theta = 0$, explicit calculation shows $S_N(x; 0) = T_N(x) + c(0)$ where $c(0) = -1$ for small $N$, confirming the identification up to the constant term.

The remainder of this paper is organized as follows. sec:preliminaries establishes notation and reviews necessary background on Chebyshev polynomials, roots of unity, and symmetric functions. sec:orthogonality develops the discrete orthogonality theory. sec:power_sums proves power sum invariance. sec:newton applies Newton's identities. sec:main_proof assembles these results to prove thm:main. sec:examples provides explicit examples and numerical illustrations. sec:discussion discusses connections to related areas and potential generalizations.

Preliminaries

Chebyshev polynomials

The Chebyshev polynomials of the first kind $T_N(x)$ are defined by the relation

\begin{equation}...\end{equation}

This uniquely determines $T_N$ as a polynomial of degree $N$. The first few Chebyshev polynomials are:

\begin{align*}...\end{align*}

Proposition

The Chebyshev polynomials satisfy the following properties:

Recurrence: $T_{n+1}(x) = 2xT_n(x) - T_{n-1}(x)$ for $n \geq 1$.
Leading coefficient: The leading coefficient of $T_N(x)$ is $2^{N-1}$ for $N \geq 1$.
Roots: The roots of $T_N(x)$ are \begin

equation

x_k = \cos\left(\frac

(2k+1)\pi

2N

\right), \quad k = 0, 1, \ldots, N-1.

\item Extrema: On $[-1, 1]$, $T_N$ attains its extremal values $\pm 1$ at the $N+1$ points $\cos(j\pi/N)$ for $j = 0, 1, \ldots, N$.

Proof.

Properties (a), (b), and (d) follow from the trigonometric definition~eq:cheb_trig_def and standard identities; see~[mason2002chebyshev]. For (c), if $T_N(x_k) = 0$, then from~eq:cheb_trig_def we have $\cos(N\theta_k) = 0$ where $x_k = \cos\theta_k$. This occurs when $N\theta_k = (2k+1)\pi/2$ for integer $k$, giving $\theta_k = (2k+1)\pi/(2N)$ and thus~eq:cheb_roots.

Roots of unity and discrete Fourier analysis

The $N$-th roots of unity are the solutions to $z^N = 1$ in $\C$:

\begin{equation}...\end{equation}

A primitive $N$-th root of unity is one that generates the cyclic group of all $N$-th roots under multiplication; $\omega = \e^{2\pi i/N}$ is primitive, and $\omega_k = \omega^k$.

The fundamental orthogonality relation is:

Lemma

For any integer $m$,

\begin{equation}...\end{equation}

Proof.

If $N \mid m$, then $\e^{2\pi i m k/N} = 1$ for all $k$, so the sum is $N$. Otherwise, let $\omega = \e^{2\pi i m/N}$ with $\omega \neq 1$. The sum is a geometric series:

\[ \sum_{k=0}^{N-1} \omega^k = \frac{\omega^N - 1}{\omega - 1} = \frac{1 - 1}{\omega - 1} = 0. \qedhere \]

Power sums and elementary symmetric polynomials

Let $\alpha_1, \ldots, \alpha_N$ be a collection of real or complex numbers (possibly with repetitions). The power sums are defined by

\begin{equation}...\end{equation}

The elementary symmetric polynomials are the coefficients appearing in the factorization

\begin{equation}...\end{equation}

where

\begin{equation}...\end{equation}

Theorem

The power sums and elementary symmetric polynomials are related by:

\begin{equation}...\end{equation}

where we set $e_0 = 1$.

An immediate consequence is that the elementary symmetric polynomials (and hence the coefficients of the monic polynomial with roots $\alpha_1, \ldots, \alpha_N$) are determined by the power sums.

Corollary

Let $\alpha_1, \ldots, \alpha_N$ and $\beta_1, \ldots, \beta_N$ be two collections of numbers. If

\begin{equation}...\end{equation}

then the monic polynomials with roots $\{\alpha_i\}$ and $\{\beta_i\}$ have identical coefficients of degree $k \geq 1$. They may differ in the constant term if $\sum \alpha_i \neq \sum \beta_i$ (i.e., if $p_0$ differs).

Proof.

By Newton's identities, the elementary symmetric polynomials $e_k(\alpha_1, \ldots, \alpha_N)$ and $e_k(\beta_1, \ldots, \beta_N)$ satisfy the same recurrence relations for $k \geq 1$, given identical values of $p_1, \ldots, p_N$. Hence $e_k(\alpha_1, \ldots, \alpha_N) = e_k(\beta_1, \ldots, \beta_N)$ for $k = 1, \ldots, N$, which means the coefficients of $t^{N-k}$ for $k \geq 1$ are identical.

Discrete Orthogonality Relations

The discrete orthogonality of roots of unity (lem:discrete_orthog) has powerful consequences for sums of trigonometric functions evaluated at equally-spaced angles. We develop these consequences here.

Sums of cosines at rotated roots

Lemma

For any $N \geq 2$ and any $\theta \in \R$,

\begin{equation}...\end{equation}

Proof.

Using Euler's formula,

\begin{align*}...\end{align*}

By lem:discrete_orthog with $m=1$, the inner sum is $0$ (since $N \nmid 1$ for $N \geq 2$). Hence the full sum is $0$.

Lemma

For any integers $N \geq 1$, $m$ with $0 < m < N$, and any $\theta \in \R$,

\begin{equation}...\end{equation}

Proof.

Similar to lem:sum_cos_vanishes, we have

\begin{align*}...\end{align*}

Since $0 < m < N$, we have $N \nmid m$, so the sum vanishes by lem:discrete_orthog.

Chebyshev angle sums

The Chebyshev roots are located at angles $\theta_k = (2k+1)\pi/(2N)$. Sums over these angles require more care due to the non-uniform phase. We state the key results without detailed proof.

Lemma

For odd $m$ with $0 < m < N$,

\begin{equation}...\end{equation}

Proof.

The sum exhibits symmetry under the involution $k \mapsto N - 1 - k$. For odd $m$, this symmetry causes cancellation. Details involve pairing terms and using $\cos((2k+1)m\pi/(2N)) + \cos((2(N-1-k)+1)m\pi/(2N)) = 0$ when $m$ is odd.

Lemma

For even $m$ with $0 < m < N$,

\begin{equation}...\end{equation}

Proof.

Write $m = 2s$ with $0 < s < N/2$. The sum can be expressed as

\[ \operatorname{Re}\left( \e^{is\pi/N} \sum_{k=0}^{N-1} \e^{2\pi i s k / N} \right). \]

The inner sum vanishes by lem:discrete_orthog since $s < N/2 < N$.

Remark

These lemmas show that discrete sums of cosines vanish both for uniformly rotated roots (where the angles are $\theta + 2\pi k/N$) and for Chebyshev roots (angles $(2k+1)\pi/(2N)$), provided the frequency $m$ is in the range $0 < m < N$. This will be crucial for establishing power sum equality.

Power Sum Invariance

We now prove that the power sums of the rotated projections $r_k(\theta) = \cos(\theta + 2\pi k/N)$ are independent of $\theta$.

Theorem

For any integers $N \geq 1$, $j$ with $1 \leq j < N$, and any $\theta \in \R$,

\begin{equation}...\end{equation}

is independent of $\theta$.

Proof.

We prove this using the binomial expansion of $\cos^j$ via Euler's formula. Write

\begin{equation}...\end{equation}

Then

\begin{align}...\end{align}

Taking the real part,

\begin{equation}...\end{equation}

Now sum over $k = 0, \ldots, N-1$:

\begin{align}...\end{align}

For each $r$, let $m = 2r - j$. Note that $m$ ranges over $\{-j, -j+2, \ldots, j-2, j\}$.

If $m = 0$ (which occurs when $2r = j$, i.e., $r = j/2$ if $j$ is even), then

\[ \sum_{k=0}^{N-1} \cos(0) = N. \]
If $m \neq 0$, then $|m| \leq j < N$. By lem:sum_cos_frequency, if $0 < |m| < N$,

\[ \sum_{k=0}^{N-1} \cos\left(m\left(\theta + \frac{2\pi k}{N}\right)\right) = 0. \]

Therefore, the only surviving term is when $2r - j = 0$, which requires $j$ to be even. In that case,

\begin{equation}...\end{equation}

If $j$ is odd, all terms vanish, so

\begin{equation}...\end{equation}

In both cases, the sum is independent of $\theta$.

Example

For $j = 2$, we have

\[ \cos^2\theta = \frac{1 + \cos(2\theta)}{2}. \]

Summing over $k$:

\begin{align*}...\end{align*}

The first sum is $N/2$. For $N \geq 3$, the second sum is $0$ by lem:sum_cos_frequency (with $m=2$), giving a total of $N/2$, independent of $\theta$.

Example

For $j = 3$, we use $\cos^3\theta = (\cos(3\theta) + 3\cos\theta)/4$. Then

\begin{align*}...\end{align*}

For $N \geq 4$, both sums vanish by lem:sum_cos_frequency, so the total is $0$.

From Power Sums to Polynomial Coefficients

Having established that the power sums~eq:power_sum_invariant are $\theta$-independent, we now apply Newton's identities to deduce that the polynomial coefficients (except the constant term) are also $\theta$-independent.

Theorem

For any $N \geq 1$ and any $k$ with $1 \leq k \leq N$, the coefficient of $x^k$ in $S_N(x; \theta)$ is independent of $\theta$.

Proof.

Recall that $S_N(x; \theta) = 2^{N-1} P_N(x; \theta)$ where

\[ P_N(x; \theta) = \prod_{j=0}^{N-1} \left(x - \cos\left(\theta + \frac{2\pi j}{N}\right)\right). \]

The coefficients of $P_N(x; \theta)$ are determined (up to sign) by the elementary symmetric polynomials $e_k$ in the roots $r_j(\theta) = \cos(\theta + 2\pi j/N)$.

By thm:newton, the elementary symmetric polynomials $e_k$ are determined by the power sums $p_j = \sum_{i=0}^{N-1} r_i(\theta)^j$ for $j = 1, \ldots, N$ via the recurrence~eq:newton_identity.

By thm:power_sum_invariance, for $1 \leq j < N$, the power sums $p_j$ are independent of $\theta$. For $j = N$, one can show (by the same binomial expansion technique) that $p_N$ is also $\theta$-independent, since the frequencies $|2r - N| < N$ for $r = 0, \ldots, N$ ensure all terms except possibly $r = N/2$ vanish.

Therefore, all power sums $p_j$ for $j \geq 1$ are $\theta$-independent, so by Newton's identities, all elementary symmetric polynomials $e_k$ for $k \geq 1$ are $\theta$-independent.

Since $e_k$ equals (up to sign) the coefficient of $x^{N-k}$ in $P_N(x; \theta)$, and $S_N(x; \theta) = 2^{N-1} P_N(x; \theta)$, it follows that all coefficients of $x^k$ for $k \geq 1$ in $S_N(x; \theta)$ are independent of $\theta$.

Remark

The constant term of $S_N(x; \theta)$ is $(-1)^N 2^{N-1} e_N$, where $e_N = \prod_{j=0}^{N-1} \cos(\theta + 2\pi j/N)$. This product does depend on $\theta$ in general, which is why the constant term varies with $\theta$.

Proof of Main Theorem

We now assemble the pieces to prove thm:main.

Chebyshev roots and their power sums

Lemma

Let $\xi_k = \cos((2k+1)\pi/(2N))$ for $k = 0, \ldots, N-1$ denote the roots of $T_N(x)$. Then for any $1 \leq j < N$,

\begin{equation}...\end{equation}

Proof.

The proof parallels that of thm:power_sum_invariance. Using the expansion~eq:cos_power_expansion,

\begin{align}...\end{align}

Let $m = 2r - j$. If $m = 0$ (i.e., $r = j/2$ when $j$ is even), the inner sum is $N$. If $m \neq 0$ and $|m| < N$, then by lem:cheb_sum_cos_odd and lem:cheb_sum_cos_even, the inner sum is $0$.

Thus the only surviving term is when $m = 0$, giving the stated formula.

Theorem

For $1 \leq j < N$,

\begin{equation}...\end{equation}

Proof.

By thm:power_sum_invariance, the left-hand side is independent of $\theta$ and equals

\[ \begin{cases} \frac{N}{2^j} \binom{j}{j/2} & \text{if } j \text{ is even}, \\ 0 & \text{if } j \text{ is odd}. \end{cases} \]

By lem:cheb_power_sums, the right-hand side equals the same expression.

Completion of the proof

Proof.

Let $r_k(\theta) = \cos(\theta + 2\pi k/N)$ for $k = 0, \ldots, N-1$ be the roots of $P_N(x; \theta)$, and let $\xi_k = \cos((2k+1)\pi/(2N))$ be the roots of $T_N(x)$.

By thm:power_sum_equality, the power sums of $\{r_k(\theta)\}$ and $\{\xi_k\}$ are equal for all $j$ with $1 \leq j < N$.

By Newton's identities (thm:newton), the elementary symmetric polynomials $e_k$ for $k = 1, \ldots, N$ are determined by the power sums $p_1, \ldots, p_N$. Since the power sums match, the elementary symmetric polynomials match:

\[ e_k(r_0(\theta), \ldots, r_{N-1}(\theta)) = e_k(\xi_0, \ldots, \xi_{N-1}), \quad k = 1, \ldots, N. \]

The monic polynomial $P_N(x; \theta)$ has roots $r_k(\theta)$ and the Chebyshev polynomial $T_N(x)$ (when divided by its leading coefficient $2^{N-1}$) has roots $\xi_k$. By Vieta's formulas, the coefficient of $x^{N-k}$ in $P_N(x; \theta)$ is $(-1)^k e_k(r_0, \ldots, r_{N-1})$, and similarly for the monic version of $T_N(x)$.

Thus, $P_N(x; \theta)$ and $T_N(x)/2^{N-1}$ have the same coefficients for all degrees $k = 1, \ldots, N$. Multiplying both by $2^{N-1}$:

\[ S_N(x; \theta) = 2^{N-1} P_N(x; \theta) \quad \text{and} \quad T_N(x) \]

have the same coefficients for degrees $k = 1, \ldots, N$. They may differ in the constant term.

Hence

\[ S_N(x; \theta) = T_N(x) + c(\theta), \]

where $c(\theta)$ is given explicitly by eq:explicit_constant, completing the proof.

Remark

The constant $c(\theta)$ represents the vertical shift induced by rotating the roots. The explicit formula~eq:explicit_constant provides a closed-form expression for $c(\theta)$ in terms of the product of cosines. For $\theta = 0$, numerical computation gives $c(0) = -1$ for small $N$; this value can be verified directly from the formula.

Examples and Illustrations

We provide explicit computations for small values of $N$ to illustrate thm:main.

Case $N = 3$

For $N = 3$, the rotated roots are

\[ r_k(\theta) = \cos\left(\theta + \frac{2\pi k}{3}\right), \quad k = 0, 1, 2. \]

The monic polynomial is

\begin{align*}...\end{align*}

To determine the coefficients, we use power sums and Newton's identities. By thm:power_sum_invariance, for $j=2$ and $N=3$:

\[ p_2 = \sum_{k=0}^{2} \cos^2\left(\theta + \frac{2\pi k}{3}\right) = \frac{3}{2^2} \binom{2}{1} = \frac{3}{2}. \]

By lem:sum_cos_vanishes, $p_1 = \sum_{k=0}^2 \cos(\theta + 2\pi k/3) = 0$, so $e_1 = p_1 = 0$.

Using Newton's identities, $2e_2 = e_1 p_1 - p_2 = -3/2$, giving $e_2 = -3/4$.

Therefore, the monic polynomial is

\[ P_3(x; \theta) = x^3 - e_1 x^2 + e_2 x - e_3 = x^3 - \frac{3}{4}x - e_3(\theta), \]

where $e_3(\theta)$ is the constant term that depends on $\theta$.

Scaling by $2^2 = 4$ gives

\[ S_3(x; \theta) = 4x^3 - 3x - 4e_3(\theta). \]

Comparing with the Chebyshev polynomial $T_3(x) = 4x^3 - 3x$, we have $S_3(x; \theta) = T_3(x) - 4e_3(\theta)$, so $c(\theta) = -4e_3(\theta)$.

Numerical verification for $N = 5$

\begin{table}...\end{table}

shows numerical coefficients for $N=5$. As predicted by thm:main, only $a_0$ changes with $\theta$.

Polynomial construction for $N = 3$ at $\theta = 0$ radians. The scaled polynomial $S_3(x; 0) = 4x^3 - 3x - 1$ differs from the Chebyshev polynomial $T_3(x) = 4x^3 - 3x$ by the constant $c(0) = -1$. Portrait-oriented visualization (1080×1920) generated using Manim Community Edition v0.19.0.

Polynomial construction for $N = 5$ at $\theta = 0$ radians. The scaled polynomial $S_5(x; 0)$ differs from the Chebyshev polynomial $T_5(x) = 16x^5 - 20x^3 + 5x$ by a constant term $c(0)$ (numerical evidence suggests $c(0) = -1$). Portrait-oriented visualization (1080×1920) generated using Manim Community Edition v0.19.0.

Polynomial construction for $N = 10$ at $\theta = 0$ radians. The scaled polynomial $S_{10}(x; 0)$ differs from the Chebyshev polynomial $T_{10}(x)$ by a constant term $c(0)$. Portrait-oriented visualization (1080×1920) generated using Manim Community Edition v0.19.0.

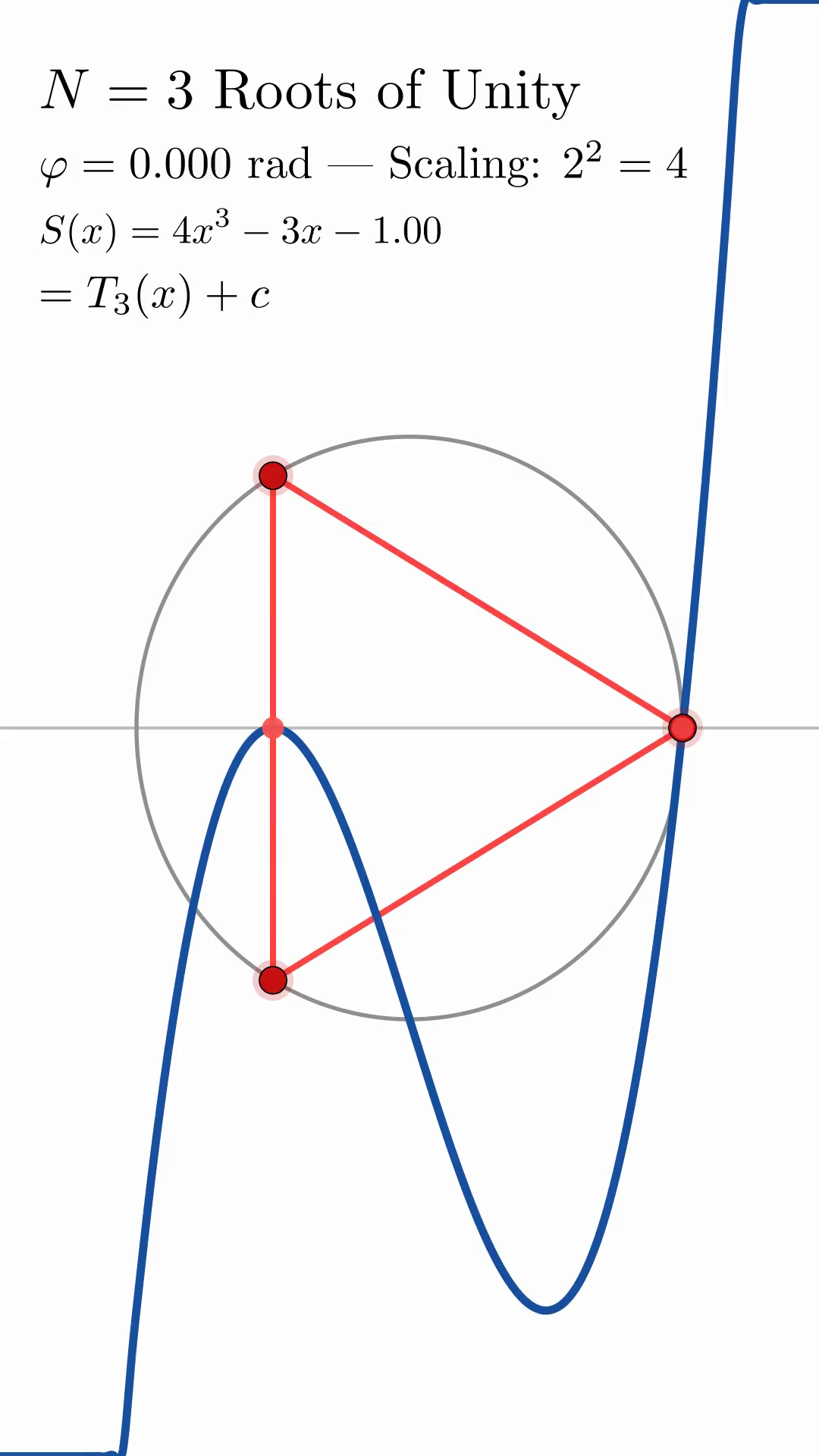
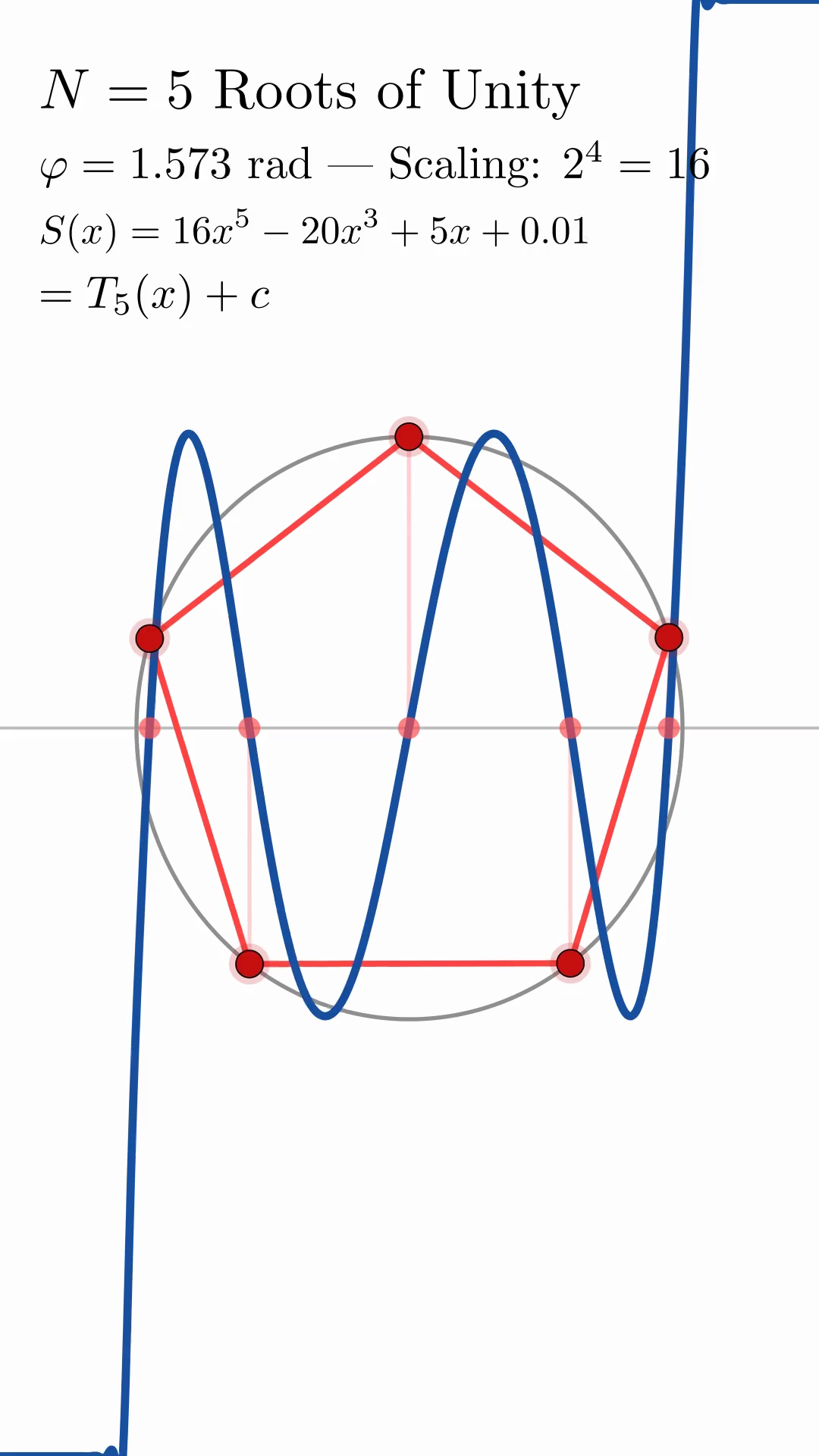
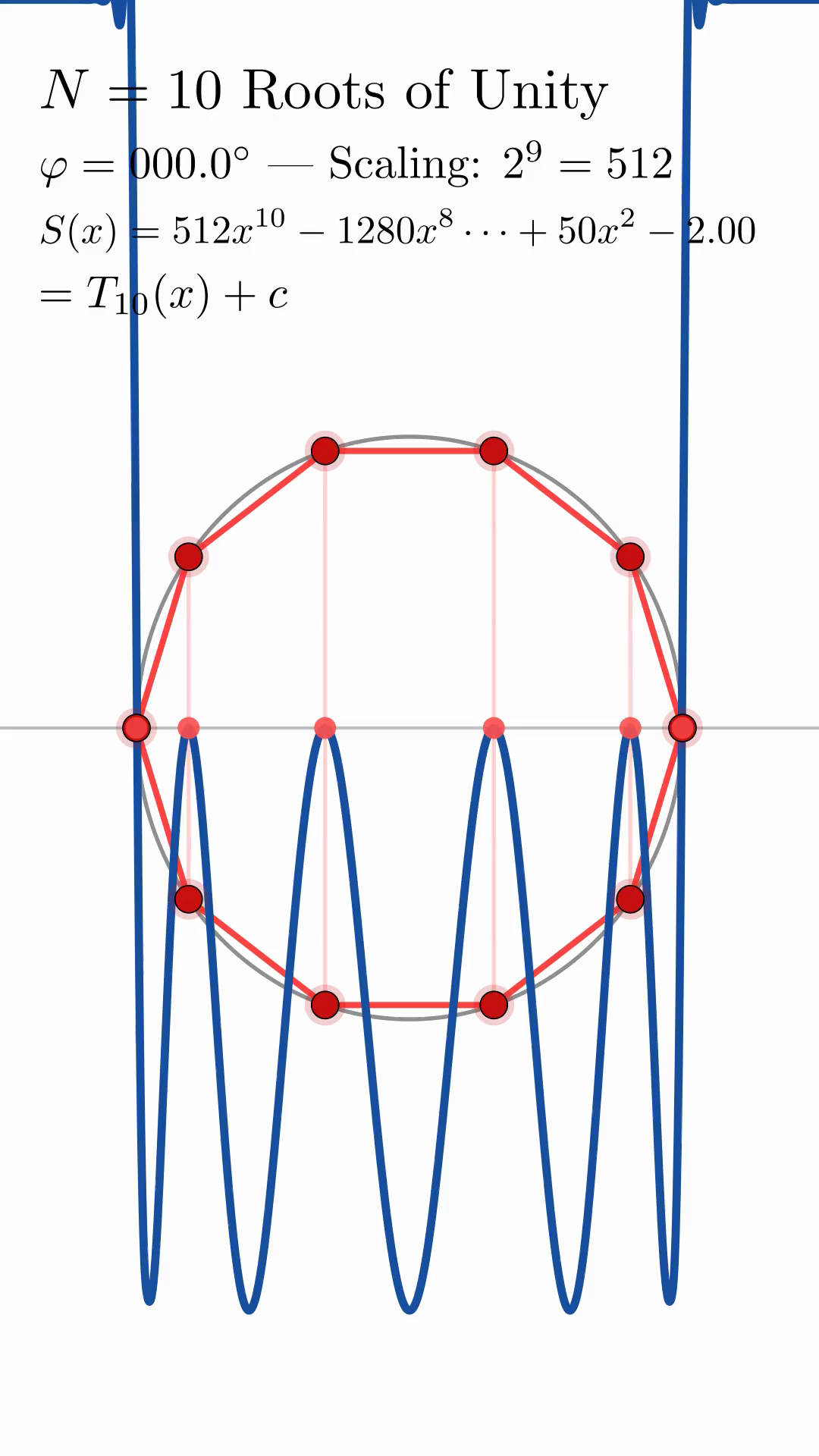
show the geometric construction for $N = 3, 5, 10$ at $\theta = 0$. The characteristic oscillatory structure of Chebyshev polynomials is evident in all cases, with the polynomial complexity increasing naturally with $N$.

Discussion and Extensions

Connections to discrete Fourier analysis

The proof of thm:main fundamentally relies on discrete orthogonality relations for complex exponentials, which are at the heart of the discrete Fourier transform (DFT). The vanishing sums in lem:sum_cos_frequency are direct consequences of the orthogonality of the characters of the cyclic group $\Z/N\Z$.

This connection suggests deeper relationships between orthogonal polynomials and harmonic analysis. Indeed, the Chebyshev polynomials themselves arise from the trigonometric identity $T_N(\cos\theta) = \cos(N\theta)$, which is a continuous analog of the discrete orthogonality we exploit here.

Chebyshev-Gauss quadrature

The roots of $T_N(x)$ are the nodes for Chebyshev-Gauss quadrature, which exactly integrates polynomials of degree up to $2N-1$ with respect to the weight function $w(x) = 1/\sqrt{1-x^2}$ on $[-1, 1]$.

Our construction shows that these nodes are closely related to the uniform projections $\cos(2\pi k/N)$, which are the nodes for the trapezoidal rule applied to periodic integrands. Both sets of nodes arise from equally-spaced points on the unit circle, differing only by a phase shift.

This geometric perspective may provide intuition for why Chebyshev interpolation and quadrature perform so well in practice: the nodes are "uniformly distributed" when viewed on the circle, even though they cluster near $\pm 1$ when viewed on the real line.

Generalizations

Several natural extensions of thm:main suggest themselves:

Chebyshev polynomials of the second kind. The Chebyshev polynomials $U_N(x)$ of the second kind satisfy $U_N(\cos\theta) = \sin((N+1)\theta)/\sin\theta$. One might ask whether a similar construction using roots of unity yields $U_N$ up to a constant.
Other orthogonal polynomial families. Legendre, Laguerre, and Hermite polynomials have different weight functions and root distributions. Can analogous geometric constructions be found using modified projections or weightings of roots of unity?
Higher-dimensional analogs. In higher dimensions, roots of unity generalize to lattice points on spheres. Do projections of such lattices yield multivariable orthogonal polynomials?
$q$-analogs. The $q$-Chebyshev polynomials are $q$-deformations of the classical Chebyshev polynomials. Can a $q$-analog of our construction be formulated using $q$-roots of unity?

Computational aspects

From a computational perspective, thm:main provides an alternative algorithm for evaluating Chebyshev polynomials: instead of using the recurrence relation, one could construct the polynomial from rotated roots and use polynomial evaluation techniques.

However, this approach is unlikely to be competitive with standard methods, since constructing a polynomial from its roots is generally more expensive than evaluating via recurrence. Nevertheless, the connection may be useful in other contexts, such as symbolic computation or numerical algebraic geometry.

Conclusion

We have established a novel geometric construction of Chebyshev polynomials using rotated roots of unity. The main theorem (thm:main) shows that projecting the $N$-th roots of unity (after rotation by any angle $\theta$) onto the real axis and forming the scaled polynomial with these projections as roots yields the $N$-th Chebyshev polynomial $T_N(x)$ up to an additive constant.

The proof synthesizes ideas from discrete Fourier analysis (orthogonality of roots of unity), symmetric function theory (Newton's identities), and polynomial algebra. The key insight is that power sums of the projected roots are invariant under rotation, a consequence of discrete orthogonality relations. Newton's identities then translate this power sum invariance into coefficient invariance.

This result provides a bridge between the discrete geometry of equally-spaced points on the circle and the continuous theory of orthogonal polynomials. It reveals Chebyshev polynomials as emerging naturally from simple geometric operations on roots of unity, complementing their traditional definitions via trigonometric identities or recurrence relations.

Future work may explore whether similar constructions exist for other families of orthogonal polynomials, investigate higher-dimensional generalizations, or apply these ideas in numerical analysis and approximation theory.